Original post is here: eklausmeier.goip.de
Installing Pallene is described in the previous post: Installing Pallene Compiler. In this post we test the performance of Pallene versus C, Lua 5.4, and LuaJIT. Furthermore we benchmark different Lua versions starting with Lua 5.1 up to 5.4.
1. Array Access. I checked a similar program as in Performance Comparison C vs. Lua vs. LuaJIT vs. Java.
1function lua_perf(N:integer, S:integer)
2 local t:{ {a:float, b:float, f:float} } = {}
3
4 for i = 1, N do
5 t[i] = {
6 a = 0.0,
7 b = 1.0,
8 f = i * 0.25
9 }
10 end
11
12 for j = 1, S-1 do
13 for i = 1, N-1 do
14 t[i].a = t[i].a + t[i].b * t[i].f
15 t[i].b = t[i].b - t[i].a * t[i].f
16 end
17 --io_write( t[1].a )
18 end
19end
This program, which does no I/O at all, runs in 0.14s, and therefore runs two times slower than the LuaJIT, which finishes in 0.07s. This clearly is somewhat disappointing. Lua 5.4, as part of Pallene, needs 0.75s. So Pallene is roughly five times faster than Lua. [more_WP_Tag]
1$ time ./lua/src/lua lua_perf/main.lua
2 real 0.14s
3 user 0.13s
4 sys 0
5 swapped 0
6 total space 0
Here, the calling main.lua routine is just
1package = require "lua_perf.lua_perf"
2N = 4000
3S = 1000
4package.lua_perf(N,S)
Runtimes are now:
- C (no optimization flags): 0.09s
- C: 0.02s
- Lua 5.1: 1.34s
- Lua 5.2: 1.49s
- Lua 5.3: 0.95s
- Lua 5.4: 0.72s
- LuaJIT: 0.07s
- Pallene: 0.14s
As explained in Pallene: A companion language for Lua, array handling in LuaJIT is still more efficient than in Pallene.
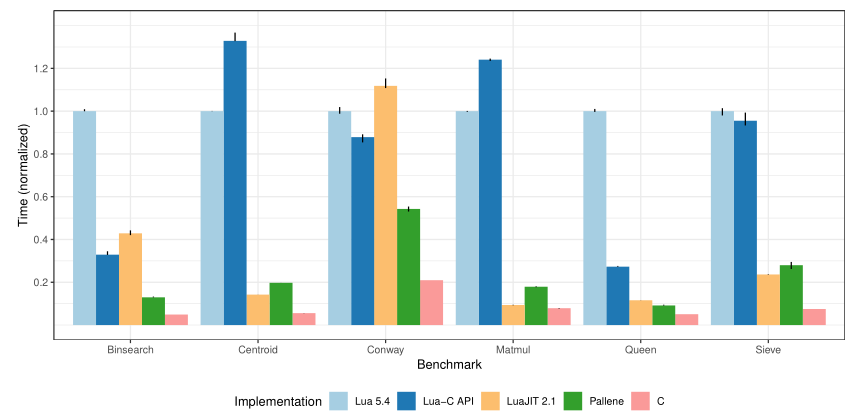
The only benchmark where LuaJIT is substantially faster than Pallene is Matmul. We have found that this difference is due to memory access. LuaJIT uses the NaN-boxing technique to pack arbitrary Lua values and their type tags inside a single IEEE-754 floating-point number [28]. In particular, this means that in LuaJIT an array of floatingpoint numbers consumes only 8 bytes per number, against the 16 bytes used by Lua and Pallene. This results in a higher cache miss rate and worse performance for Pallene.
2. Integer Computation. Below program computes the number of configurations for multiple chess queens to be positioned without attacking each other. It is the well known n-queen problem. Often times this is solved in a recursive fashion, but the most obvious program is non-recursive and uses goto-statements. Below code is in xdamcnt2.c on GitHub.
1#define abs(x) ((x >= 0) ? x : -x)
2
3/* Check if k-th queen is attacked by any other prior queen.
4 Return nonzero if configuration is OK, zero otherwise.
5*/
6//inline --> not faster, klm, 24-Apr-2020
7int configOkay (int k, int a[]) {
8 int z = a[k];
9
10 for (int j=1; j<k; ++j) {
11 int l = z - a[j];
12 if (l == 0 || abs(l) == k - j) return 0;
13 }
14 return 1;
15}
16
17long solve (int N, int a[]) { // return number of positions
18 long cnt = 0;
19 int k = a[1] = 1;
20 int N2 = N; //(N + 1) / 2;
21
22 loop:
23 if (configOkay(k,a)) {
24 if (k < N) { a[++k] = 1; goto loop; }
25 else ++cnt;
26 }
27 do
28 if (a[k] < N) { a[k] += 1; goto loop; }
29 while (--k > 1);
30 a[1] += 1;
31 if (a[1] > N2) return cnt;
32 k = 2 , a[2] = 1;
33 goto loop;
34}
Compiled the program with all optimization (-march=native -O3), then ran this program.
1$ time xdamcnt2 1 12
2 n-queens problem.
3 2 4 6 8 10 12 14
4 1 0 0 2 10 4 40 92 352 724 2680 14200 73712 365596
5
6 D( 1) = 1
7 D( 2) = 0
8 D( 3) = 0
9 D( 4) = 2
10 D( 5) = 10
11 D( 6) = 4
12 D( 7) = 40
13 D( 8) = 92
14 D( 9) = 352
15 D(10) = 724
16 D(11) = 2680
17 D(12) = 14200
18 real 0.21s
19 user 0.21s
20 sys 0
21 swapped 0
22 total space 0
Above C code has been translated to Lua 5.1, which does not provide goto-statements. We deliberately chose Lua 5.1, because LuaJIT can only handle Lua 5.1 syntax. Only starting with Lua 5.2 the goto-statement is allowed in Lua. Not having a goto-statement required to use auxiliary variables, here called flag, then checking with if-statements. This file is called xdamcnt2.lua on GitHub.
1-- Check if k-th queen is attacked by any other prior queen.
2function configOkay (k, a)
3 local z = a[k]
4 local kmj
5 local l
6
7 for j=1, k-1 do
8 l = z - a[j]
9 kmj = k - j
10 if (l == 0 or l == kmj or -l == kmj) then
11 return false
12 end
13 end
14 return true
15end
16
17function solve (N, a) -- return number of positions
18 local cnt = 0
19 local k = 1
20 local N2 = N --(N + 1) / 2;
21 local flag
22 a[1] = 1
23
24 while true do
25 flag = 0
26 if (configOkay(k,a)) then
27 if (k < N) then
28 k = k + 1; a[k] = 1; flag = 1
29 else
30 cnt = cnt + 1; flag = 0
31 end
32 end
33 if (flag == 0) then
34 flag = 0
35 repeat
36 if (a[k] < N) then
37 a[k] = a[k] + 1; flag = 1; break;
38 end
39 k = k - 1
40 until (k <= 1)
41 if (flag == 0) then
42 a[1] = a[1] + 1
43 if (a[1] > N2) then return cnt; end
44 k = 2; a[2] = 1;
45 end
46 end
47 end
48end
The Lua code was then translated to Pallene by adding the required types to each variable. This translation is straightforward. File is called xdamcnt2.pln on GitHub.
1-- Check if k-th queen is attacked by any other prior queen.
2function configOkay (k:integer, a:{integer}):boolean
3 local z:integer = a[k]
4 local l:integer
5 local kmj:integer
6
7 for j=1, k-1 do
8 l = z - a[j]
9 kmj = k - j
10 if (l == 0 or l == kmj or -l == kmj) then
11 return false
12 end
13 end
14 return true
15end
16
17function solve (N:integer, a:{integer}):integer -- return number of positions
18 local cnt:integer = 0
19 local k:integer = 1
20 local N2:integer = N --(N + 1) / 2;
21 local flag:integer
22 a[1] = 1
23
24 while true do
25 flag = 0
26 if (configOkay(k,a)) then
27 if (k < N) then
28 k = k + 1; a[k] = 1; flag = 1
29 else
30 cnt = cnt + 1; flag = 0
31 end
32 end
33 if (flag == 0) then
34 flag = 0
35 repeat
36 if (a[k] < N) then
37 a[k] = a[k] + 1; flag = 1; break;
38 end
39 k = k - 1
40 until (k <= 1)
41 if (flag == 0) then
42 a[1] = a[1] + 1
43 if (a[1] > N2) then return cnt; end
44 k = 2; a[2] = 1;
45 end
46 end
47 end
48end
Runtimes are now:
- C (no optimization flags): 0.53s
- C: 0.2s
- Lua 5.1: 6.15s
- Lua 5.2: 7.2s
- Lua 5.3: 5.83s
- Lua 5.4: 3.92s
- LuaJIT: 0.58s
- Pallene: 0.32s
- Pallene with compiler optimization flags: 0.31s
This time Pallene is two times faster than LuaJIT, and it is 13-times faster than Lua 5.4. Additionally we observe that Lua 5.4 is faster than all previous versions by a large margin. Interesting enough, the C program only needs 60% of the Pallene running time.
3. Environment. All tests were done on an AMD FX-8120 Octacore processor with max. 3.1 GHz. This processor has 64 KiB L1 data cache.
1$ lscpu
2Model: 1
3Model name: AMD FX(tm)-8120 Eight-Core Processor
4CPU max MHz: 3100.0000
5CPU min MHz: 1400.0000
6L1d cache: 64 KiB
7L1i cache: 256 KiB
8L2 cache: 8 MiB
9L3 cache: 8 MiB
This CPU runs Arch Linux 5.6.6 and gcc 9.3.0.
Above runtime comparisons are in line with the benchmarks in Pallene: A companion language for Lua.
Added 17-Jul-2020: Cited in LWN: What's new in Lua 5.4.
Added 27-Nov-2022: A strong contender to replace LuaJIT might be Haoran Xu's LuaJIT Remake (LJR).
Added 30-Oct-2023: Referenced in Dragonfly + BullMQ = massive performance. Dragonfly is a faster Redis variant, BullMQ is a Node.js library with queuing.