Original post is here: eklausmeier.goip.de
Our solar system is not stable when considerung time ranges of several Gigayears. These are the results of simulations done by Laskar and Gastineau.
1. Nomenclature #
Notions for ellipses, see below figure:
- center M
- semi-minor axis b
- semi-major axis a
- (linear) eccentricity e, numerical eccentricity $\varepsilon$
$$ \pmatrix{x(t)\cr y(t)} = \pmatrix{a \cos(t)\cr b \sin(t)}, \qquad \varepsilon = {e\over a} = {\sqrt{a^2-b^2}\over a} = \sqrt{1 - \left({b\over a}\right)^2} $$ The numerical eccentricity describes by "how much" the shape of the ellipse differs from a circle: a value of zero means it is a circle, anything large than zero becomes more deformed.
Below are the numerical eccentricities of the planets in our solar system. Semi-minor and semi-major axes length are given in AU.
| Nr. | Planet | Eccentricity | a | b | #moons |
|---|---|---|---|---|---|
| 1 | Mercury | 0.206 | 0.38700 | 0.37870 | 0 |
| 2 | Venus | 0.007 | 0.72300 | 0.72298 | 0 |
| 3 | Earth | 0.017 | 1.00000 | 0.99986 | 1 |
| 4 | Mars | 0.093 | 1.52400 | 1.51740 | 2 |
| 5 | Jupiter | 0.049 | 5.20440 | 5.19820 | 95 |
| 6 | Saturn | 0.057 | 9.58250 | 9.56730 | 146 |
| 7 | Uranus | 0.046 | 19.21840 | 19.19770 | 28 |
| 8 | Neptune | 0.010 | 30.11000 | 30.10870 | 16 |
2. The Jovian Planets #
Below text is from The Jovian Planets:
The four Jovian planets — Jupiter, Saturn, Uranus, and Neptune — are also called "giant planets". The Jovian planets occupy orbits in the outer solar system at distances ranging from 5 (Jupiter) to 30 (Neptune) times the Earth’s distance from the Sun. ...
Unlike the terrestrial planets that make up our inner solar system — Mercury, Venus, Earth, and Mars — the Jovian planets do not have solid surfaces. Instead, they are composed primarily of hydrogen and helium, with traces of methane, ammonia, water, and other gases in their atmospheres. These gases make up a deep atmosphere and become tightly compressed around relatively tiny cores of rock. At great depths within Jupiter, for example, the hydrogen gas is compacted so tightly that it exists in a rare metallic form.
3. Jovian problem #
Below text is from N-body simulations: the performance of eleven integrators by P.W. Sharp.
The Jovian problem has the Sun, Jupiter, Saturn, Uranus and Neptune interacting through classical Newtonian gravitational forces. Let ${\bf r}_i$ denote the position of the i-th body, where the bodies are ordered Sun to Neptune and the coordinate system is three-dimensional Cartesian with the origin at the barycenter of the bodies. G is the gravitational constant, $m_i$ is the i-th mass. The differential equation is $$ \ddot{\bf r}i(t) = \sum{j=1\atop j\ne i}^5 { G m_j ({\bf r}_j(t) - {\bf r}_i(t) \over \left\Vert {\bf r}_j(t) - {\bf r}_i(t) \right\Vert^2 }, \qquad i=1,\ldots,5. $$ Except for the emission of Pluto and a change in the coordinate system, above equation is problem C5 from Nonstiff DETEST.
This problem becomes particularly demanding when the integration interval is long, e.g., ten million years.
A simple test for correctness is to use the total energy: $$ E = {1\over2} \left[ \sum_{i=1}^5 \left( m_i {\bf r}i^2 - \sum{j=1\atop j\ne i}^5 { G m_i m_j \over \left\Vert {\bf r}_j - {\bf r}_i \right\Vert } \right) \right]. $$ Total energy E must be constant over all time t. It is a not a very accurate measure for correctness.
Above paper gives more involved differential equations for:
- Nine planet problem
- Spin Axis problem
- DE102 problem
4. Evolution of planetary orbits #
Below text is from Laskar: Stability of the solar system.
For all external planets, the maximum eccentricity is almost constant. That reflects the fact that these trajectories are very close to regular and quasiperiodic trajectories; possible instabilities are insensitive with the scale of the drawing.
For Venus and the Earth, one observes moderated variations, but still significant. The maximum eccentricity of the Earth reached through chaotic diffusion reaches about 0.08, whereas its current variations are approximately 0.06. It is about the same for Venus.
It should however be noted that to arrive at this possible collision between Mercury and Venus, the model was used beyond its rigorous field of validity, which does not includes the vicinity of collisions. In addition, the solution was carefully chosen, so in any case, it is surely not a very probable one, and the majority of the solutions of close initial conditions will not lead to this possible collision.
Concerning the system of the outer planets, the things are appreciably different, because the direct gravitational short period perturbations are more significant. The recent numerical simulations show that particles placed among the outer planets do not remain beyond a few hundreds of million years, apart for some particular zones of stability or beyond Neptune, in the Kuiper belt, where objects explicitly were found.
Finally, these observations also make it possible to have an idea of the general aspect of a planetary system around a star. Indeed, if the process of formation planetary from planetesimals is correct, it becomes possible that the planetary systems will always be in a state of marginal stability, like our own Solar system. At the end of the phase of formation of the system, a large number of bodies can remain, but in this case the system is strongly unstable, which will led to a collision or an ejection. After this event, the system becomes more stable, with constantly, a time of stability comparable with its age.
5. Instability of solar system after 3 Gyr #
Mogavero, Hoang and Laskar use below Hamiltonian $$ \hat H = - \sum_{i=1}^8 \left[ \sum_{\ell=1}^{i-1} \left\langle { G m_i m_\ell \over \left\Vert {\bf r}i - {\bf r}\ell \right\Vert } \right\rangle + { 3 G^2 m_0^2 m_i \over c^2 a_i^2 \sqrt{1-\varepsilon_i^2} } \right] . $$ Notation:
- The $a_i$ are the semi-major axes.
- $m_0$ and $m_i$ are the masses of Sun and the planets.
- $\varepsilon_i$ are the eccentricities of the planets.
- The ${\bf r}_i$ are the heliocentric positions of the planets.
- c is the speed of light.
- The bracket operator represents the averaging over the mean longitudes resulting from the elimination of non-resonant Fourier harmonics of the N-body Hamiltonian.
See Mogavero+Laskar: Long-term dynamics of the inner planets in the Solar System.
The text Stability of the solar system shows below results for the eccentricity of Mercury after 1-5 Gyr.
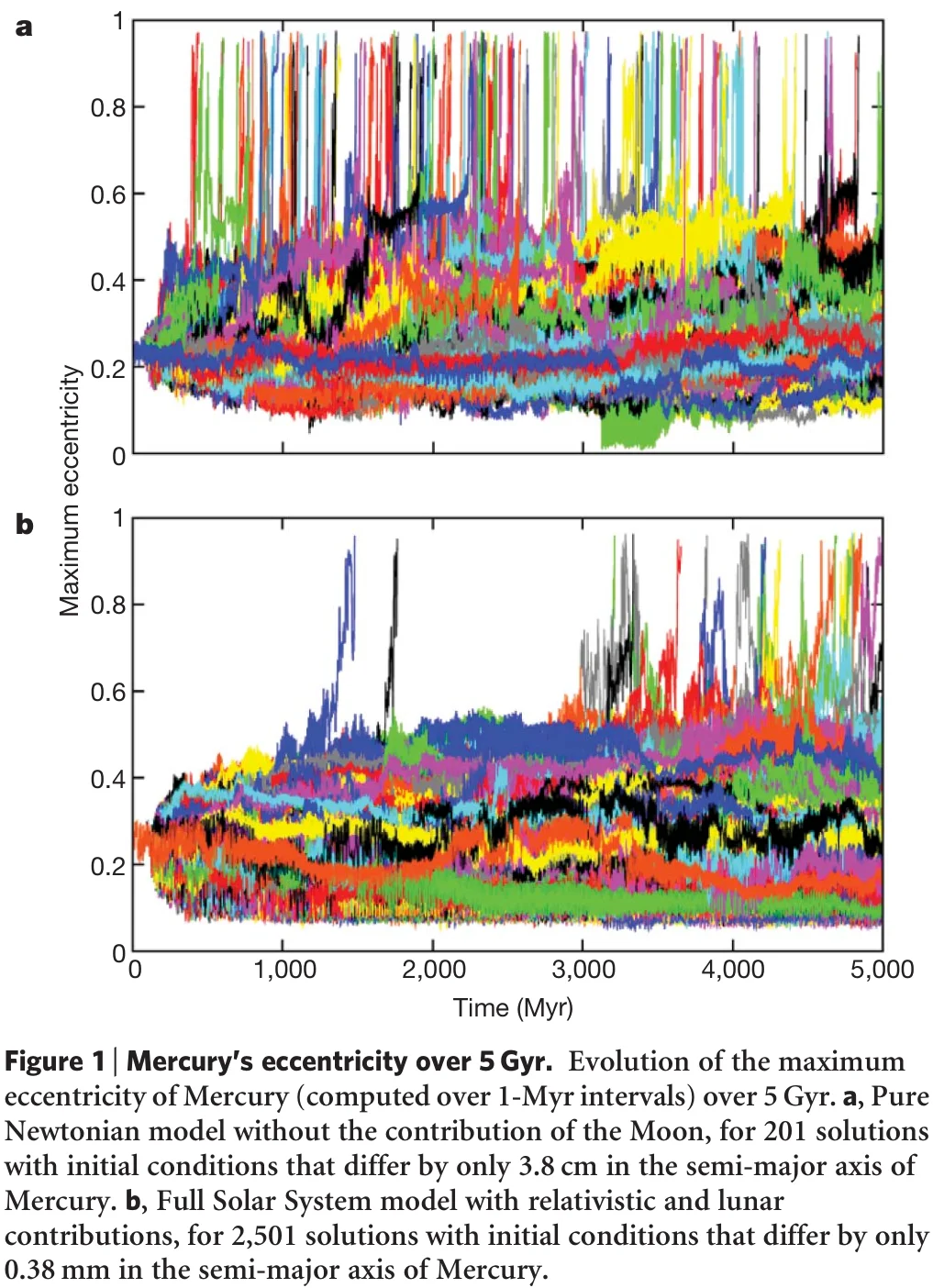
Thanks to relativity the eccentricities of Mercury stay way lower than ignoring relativity. Nevertheless, after around 1Gyr the solar system becomes destabilized by Mercury crashing into Venus, statistically speaking, i.e., in 1% of cases this can happen.
Beyond this spectacular aspect, these results also validated the methods of semi-analytical averaging developed for more than 20 years and which had allowed to show the possibility of collision between Mercury and Venus (Laskar, 1994). These results also answer to the question raised more than 300 years ago by Newton, by showing that collisions among planets or ejections are actually possible within the life expectancy of the Sun, that is, in less than 5 Gyr. The main surprise that comes from the numerical simulations of the recent years is that the probability for this catastrophic events to occur is relatively high, of the order of 1%, and thus not just a mathematical curiosity with extremely low probability values. At the same time, 99% of the trajectories will behave in a similar way as in the recent past millions of years, which is coherent with our common understanding that the Solar System has not much evolved in the past 4 Gyr. What is more surprising is that if we consider a pure Newtonian world, starting with the present initial conditions, the probability of collisions within 5 Gyr grows to 60%, which can thus be considered as an additional indirect confirmation of general relativity.
Also see:
- Long-term instability of the inner Solar system: numerical experiments
- Timescales of Chaos in the Inner Solar System: Lyapunov Spectrum and Quasi-integrals of Motion by Federico Mogavero, Nam H. Hoang,and Jacques Laskar
